 Az elmúlt napokban, hetekben újból előtérbe kerültek a könyvelési, értékesítési csalások, amelyek egy-egy részvény árfolyamát akár végérvényesen is kivégezhetik. Sok elemzőház, hedge fund szakosodott arra, hogy az ilyen vállalatokat megtalálja és aztán short pozícióval, (azaz a részvény eladásával, majd későbbi időpontban alacsonyabb áron történő visszavételével) nyereségre tegyen szert. A 2000-es évek elején a nagy vihart az Enron és a Worldcom botránya szolgáltatta, az utóbbi hónapokban a Ryanair és a Valeant Pharma került az előtérbe.
Az elmúlt napokban, hetekben újból előtérbe kerültek a könyvelési, értékesítési csalások, amelyek egy-egy részvény árfolyamát akár végérvényesen is kivégezhetik. Sok elemzőház, hedge fund szakosodott arra, hogy az ilyen vállalatokat megtalálja és aztán short pozícióval, (azaz a részvény eladásával, majd későbbi időpontban alacsonyabb áron történő visszavételével) nyereségre tegyen szert. A 2000-es évek elején a nagy vihart az Enron és a Worldcom botránya szolgáltatta, az utóbbi hónapokban a Ryanair és a Valeant Pharma került az előtérbe.
Az ilyen „félre”könyveléseket azonban egészen nehéz kiszúrni, hiszen ahhoz jól kell ismerni a vállalatok mérlegét, az iparági sajátosságokat, figyelni kell a cégek nyilatkozatait, tehát ez egy elég hosszadalmas munka, melynek folyamán valószínűleg a vállalat az állításunk ellenkezőjét fogja foggal-körömmel bizonyítani, vagyis, hogy mindent tökéletesen csinált. Szóval, közel sem biztos, hogy a kutatómunka gyümölcse beérik.
Azonban van egy egyszerűbb módja is annak, hogy megtudjuk, ha valami nem megfelelően működik.
Az egész Benford törvényéhez kötődik. Frank Benford amerikai fizikus volt, aki azt vette észre 1938-ban, hogy a könyvtári logaritmus táblázatok első oldalai jobban el vannak használódva, mint a későbbiek.
Ezen a gondolaton továbbhaladva kimutatta, hogy a mindennapok során használatos számok sokkal gyakrabban kezdődnek 1-gyel, mint 9-cel. Egészen pontosan a számok 31%-a kezdődik 1-gyel, 19%-uk 2-vel és 12% 3-mal. Ezt sok helyen ellenőrizték, például tőzsdén, számlákon, utcai címeken, időjárási adatokon, városok populációin, születési és halálozási statisztikákon, és a korábban ismertetett eloszlás igaznak bizonyult.
Benford törvényét még az amerikai adóhatóság (IRS) is használja arra, hogy kiszűrje, kik azok, akik valószínűleg adót csalnak. Az első három szám kétszer olyan gyakori, mint a 4 és 9 közötti összes szám. (Érdekes, hogy a 0 előfordulási valószínűsége elenyésző.)
Ha a legtöbb helyen működik, akkor mi lenne, ha használnák vállalatok ellenőrzésére? A Deutsche Bank ezen a vonalon indult el, és különböző vállalatok beszámolóit vizsgálta mega Benford törvény alapján. Ha egy adott vállalat könyvelése nem illeszkedik a Benford törvényhez, akkor ott vagy csalás, vagy félrekönyvelés, esetleg emberi hiba, mulasztás történhetett. A Deutsche Bank a Russell 3000 tagjait elemezte. Ez a 3000 vállalat az amerikai piac kapitalizációjának 98%-át adja, azaz szinte lefedi a részvénypiacot.
A vizsgálat alapján két portfóliót vettek alapul. Az egyik maga az index, a Russell 3000 volt, a másik pedig a piaci kapitalizáció alapján súlyozott olyan portfólió, amely olyan cégeket tartalmazott, amelyek könyvelése nem illett a fent említett Benford törvénybe. A két portfólió 1999-ben kezdett szétválni, amint az az ábrán is látható, és a törvénybe nem illő vállalatok jelentősen alulteljesítették a részvénypiacokat (világos kék diagram mutatja a törvénybe nem illő vállalatokból alkotott portfóliót).
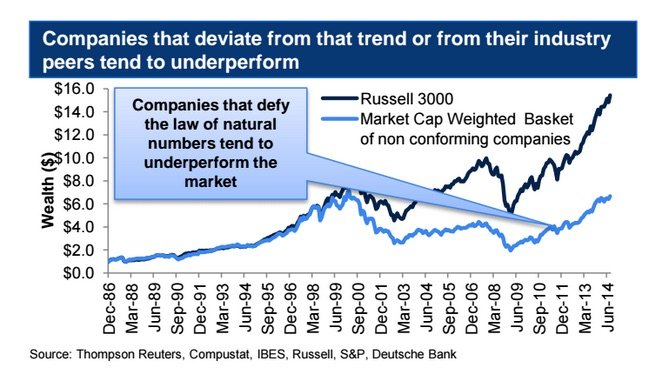
Az 1990-2000-es években megfigyelhető szétválás talán érthető is, hiszen a dotcom lufival érkezett el az az időszak, amikor megszaporodtak a csalások. A 3000 amerikai vállalat 5%-ánál lehetett valami fiaskót felfedezni ezután. Példakánt említik, hogy az Enronnál az 5, 6 és a 7-es szám sokkal többször fordult elő, mint arra következtetni lehetne a törvényből.
A fent felvázolt stratégia persze nem azt jelenti, hogy minden körülmények között megjátszható és működik is, de talán arra jó, hogy elgondolkozzunk, és jobban megvizsgáljuk egy adott vállalat fundamentumait.
Címkék: statisztika pletyka szerencse bank stratégia elemzés trend érdekesség tőzsde esélyek előrejelzés guru elemzők árbevétel portfólió volatilitás kockázatkezelés besorolás szentiment equilor adatelemzés Russell2000 tulajdonosi struktúra prudens működés eqa benford
A bejegyzés trackback címe:
Kommentek:
A hozzászólások a vonatkozó jogszabályok értelmében felhasználói tartalomnak minősülnek, értük a szolgáltatás technikai üzemeltetője semmilyen felelősséget nem vállal, azokat nem ellenőrzi. Kifogás esetén forduljon a blog szerkesztőjéhez. Részletek a Felhasználási feltételekben és az adatvédelmi tájékoztatóban.















